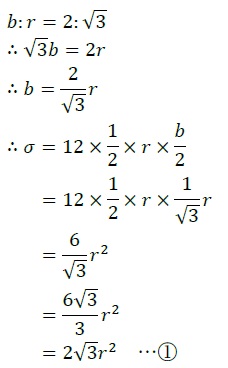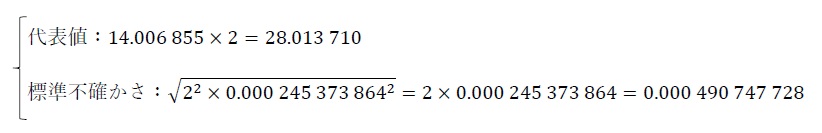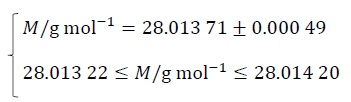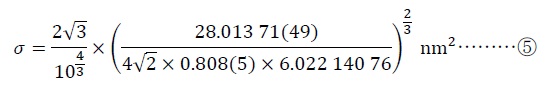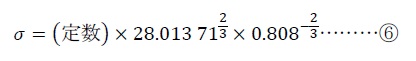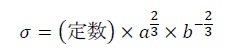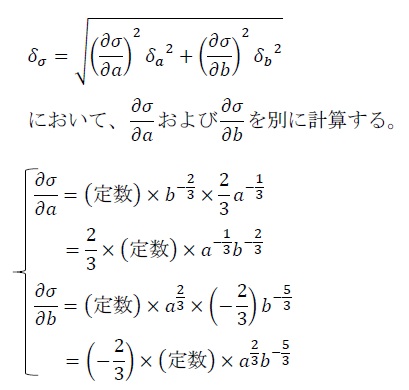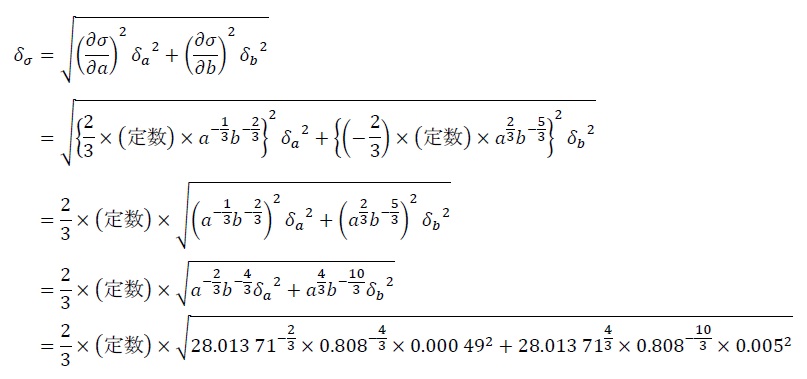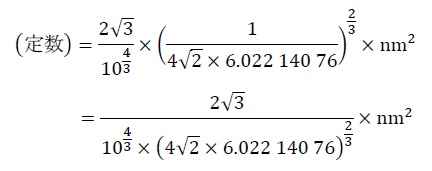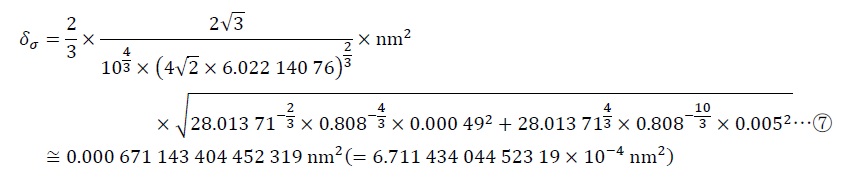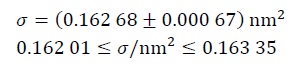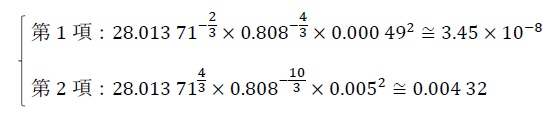0006. 化学(物理化学)：窒素の物理吸着における分子占有断面積の算出。

戻る

2025年3月13日掲載、2025年7月12日更新

■問■
　液体窒素温度における窒素の吸着現象を利用した、固体物質の表面積の測定の際に必要な、窒素の分子占有断面積σを表す式を、
  1. 吸着分子は球形である。
  2. 吸着分子は固体表面上では面心立方で最密充填している。
  3. 吸着分子の半径は、吸着温度における通常の液体あるいは固体の分子半径に等しい。
と仮定して導出し、その値を求めよ。

■解答例■
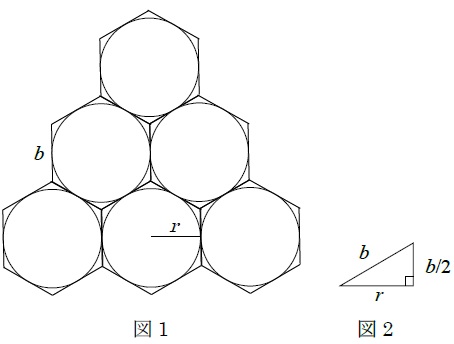
　図1に示すように、1個の吸着分子は1個の正6角形に相当する面積を有する。図2より、
図1・図2
式群1
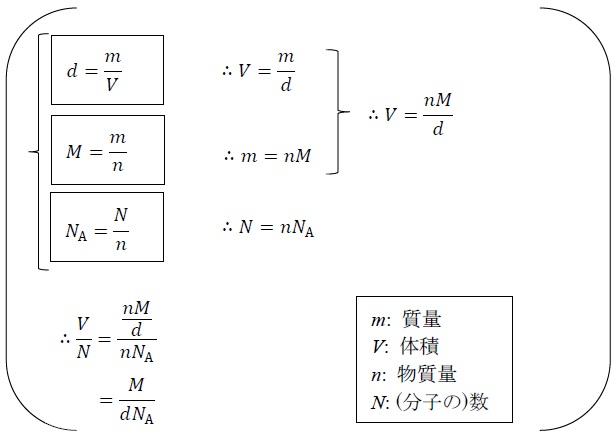
　吸着物質の密度をd、吸着物質のモル質量をM、アボガドロ定数をNAとすると、吸着分子1個当たりの体積V/Nは、M/(dNA)となる。
式群2
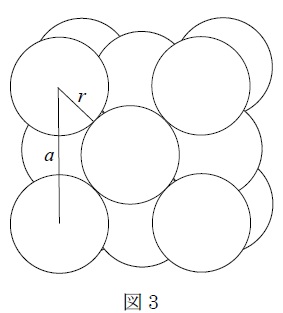
　吸着分子は図3のように面心立方で最密充填していると仮定しているので、立方体の各頂点と各面の中心を吸着分子が占めることになるから、単位格子には平均4個の分子がおさまり、その体積は4M/(dNA)となる。
図3
　単位格子の1辺の長さをaとすると、aは対角線の長さ4rの正方形の1辺である。したがって、
式群3
③の各物理量を各々の単位で割った形に変形すると、
式群4
　ここで、M、dおよびNAの値を求める。Mは日本化学会の原子量表(2025)を、dは種々の文献で報告されているものを、NAはBIPM（国際度量衡局。[仏]Le Bureau international des poids et mesures）の「7つの定義定数」の一つとして公表されているものを元にすることにする。

　まずMの値を求める。日本化学会の原子量表(2025)で与えられている窒素の原子量から、窒素分子（N2）のモル質量を求める。

　原子量表では、窒素の原子量については、
[14.006 43, 14.007 28]
と与えられている。これは、表の注記に従うと、原子量が、それぞれの元素を構成している安定核種の相対存在度（元素の同位体比）に依存することによって、その元素（今の場合窒素）を含む物質の起源や処理の仕方などによって変わりうることを背景とした、原子量の変動範囲を表している。表中の窒素の「注」の欄には、"m"の記号、すなわち「人為的な同位体分別を受けた試薬が一般的に利用されている可能性がある」ことが記されている。

　また、分子量（分子のモル質量を単位「g mol-1」で除した値）などを計算する場合の注として、上限・下限自体の値は不確かさを持っていないこと、対象とする元素について由来等の情報がなく、原子量表のみから計算する場合は、不確かさや変動範囲で示されている範囲に真の原子量が同じ確率で存在すると考える（長方形分布）こと、とされている。この場合、計算で用いる原子量の代表値は、変動範囲を[a, b]とすると(a+b)/2であり、標準不確かさは(b-a)/2√3となり、分子量などを計算する場合は、上記の代表値と標準不確かさを用いて誤差の伝播の式によって求める、とある。

　以上の前提に従うと、窒素の原子量は、
式群5
となる。そして、窒素分子（N2）の分子量は、
式群6
より、
28.013 71(49)
と表される。よって、
M/g mol-1 = 28.013 71(49)
となる。ここで、「28.013 71(49)」は、最後の「71」の桁に「49」だけの不確かさがあることを示す。すなわち、
式群7
と同じ意味である。

　次にd/g cm-3の値であるが、これは種々の文献で、0.807、0.808、0.809または0.81の値が報告されている。筆者が調べたところ「0.808」の報告が最も多かったので、この値を採用する。これは測定値と判断できるが、いずれの文献の報告にも精度に関して特に断りがなかったので、最後の桁の不確かさを大きく見積もって、仮に「0.005」として計算することにする。すると、
d/g cm-3 = 0.808(5)
となる。

　最後にNAであるが、これは上述したように、BIPMが公表しているものを用いる。これは不確かさがまったくない定義値であるので、正確に
NA/1023 mol-1 = 6.022 140 76
である。以上をまとめると、
式群8
となる。式④にこれらの値を代入すると、
式群9
となる。
　「28.013 71」と「0.808」以外は不確かさのない値なので、
式群10
のように表せる。ここで、
式群11
とおくと、
式群12
と表せる。さらに、誤差の伝播の式
式群13
よって、
式群14
となる。また、「（定数）」の部分は、式⑤および⑥より
式群15
となるので、全体を省略せずに書くと、
式群16
と計算できる。式⑤より、σの代表値は
σ≒0.162 684 511 335 616 nm2
となるので、これらの結果から、
σ=0.162 68(67) nm2
となる、という帰結である。これは、
式群17
と同じ意味である。

　ここで、この値の精度を考えてみる。これまでの値の計算の中で、「d/g cm-3」の値を考えるときに、その精度（標準不確かさ）が不明であったので、仮にそれを大きめに「0.005」と見積もった。式⑦で根号の中の第1項と第2項を計算すると、
式群18
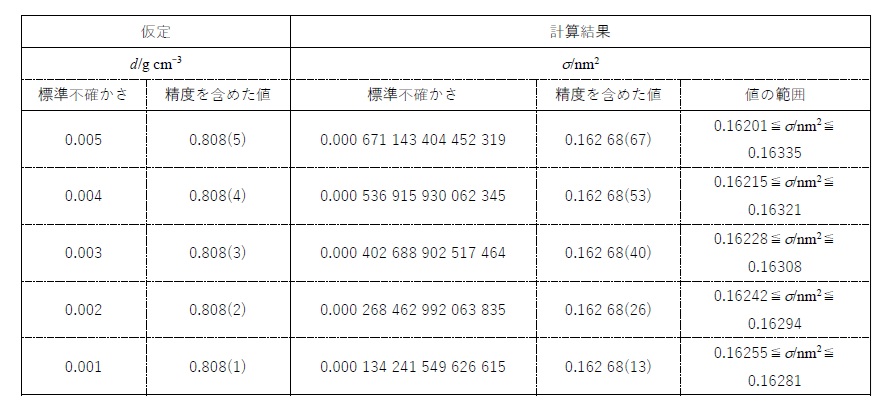
という値となり、第1項は無視できるほどに小さい。すなわち、第2項の中の不確かさ「0.005」の変動は、「d/g cm-3」の不確かさの値に与える影響が大きいことが分かる。ここで、この「0.005」の値を、「0.004」、…、「0.001」と変化させて全体の結果を計算してみると、次の通りとなった。
表1
我が国の初等・中等教育において、測定値の精度を考えるとき、有効数字の桁数というものが用いられ、特に断りのない場合には、末尾の桁の数値が±1程度の不確かさを持つ、とされているが、今回のこの「d/g cm-3」すなわち液体窒素温度での窒素の密度の値の精度は、前述したように0.807、0.808、0.809または0.81と報告値が変動することからも分かるように、±1よりもずっと大きい可能性が考えられる。

　上の表から、「σ/nm2」すなわち分子占有断面積の値は、不確かさを大きく見積もっても、おおよそ0.162台の前半から0.163台の前半辺りの間に含まれるようである。比表面積の比較的大きい固体物質において吸着質として用いられる窒素の分子占有断面積の値は、日本産業規格(JIS)の文書を始め、ほとんどの技術文書においても「0.162 nm2」という値が記されており、BET法（Brunauer-Emmett-Tellerの吸着等温線に基づいた吸着の理論を応用した表面積測定法）では、気体の吸着量に分子占有断面積を乗じて表面積を求めるという原理になっている。当然、分子占有断面積の値が変われば、表面積の値も変わってくることになる。「0.162 nm2」という値の信頼性を、今一度考えてみる価値がありそうである。

【参考文献】
慶伊富長、「共立全書157　吸着」、共立出版(株)・1965年発行。

戻る

Copyright(C) 2017 KONISHI, Shoichiro. All rights reserved.