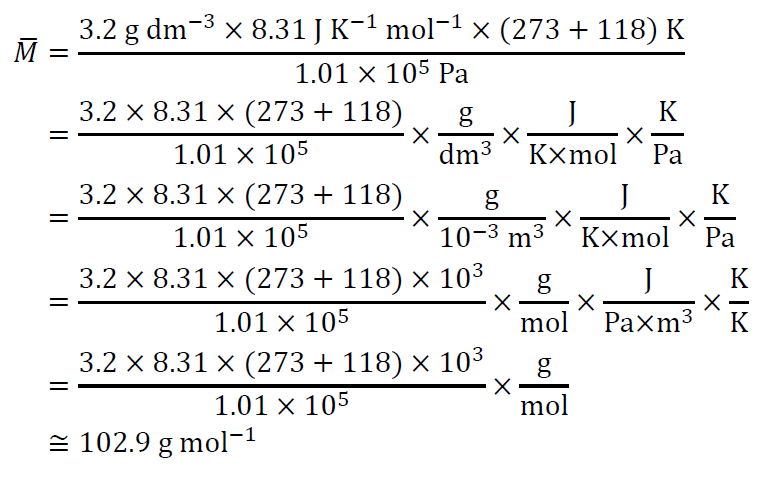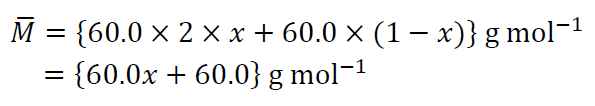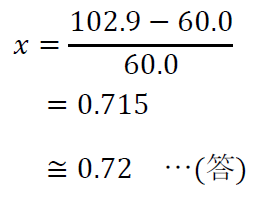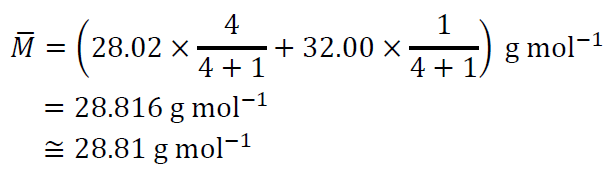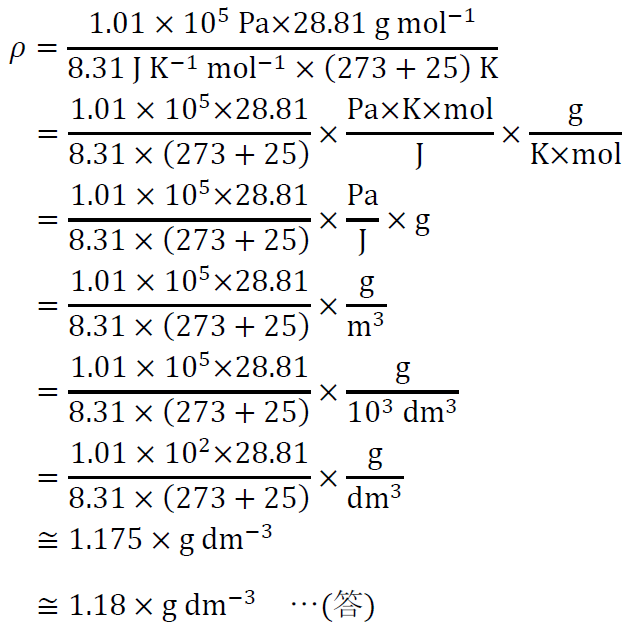0001. 化学(物理化学)：理想気体の状態方程式の応用、モル質量・密度を求める。

2024年3月3日掲載

【解説】
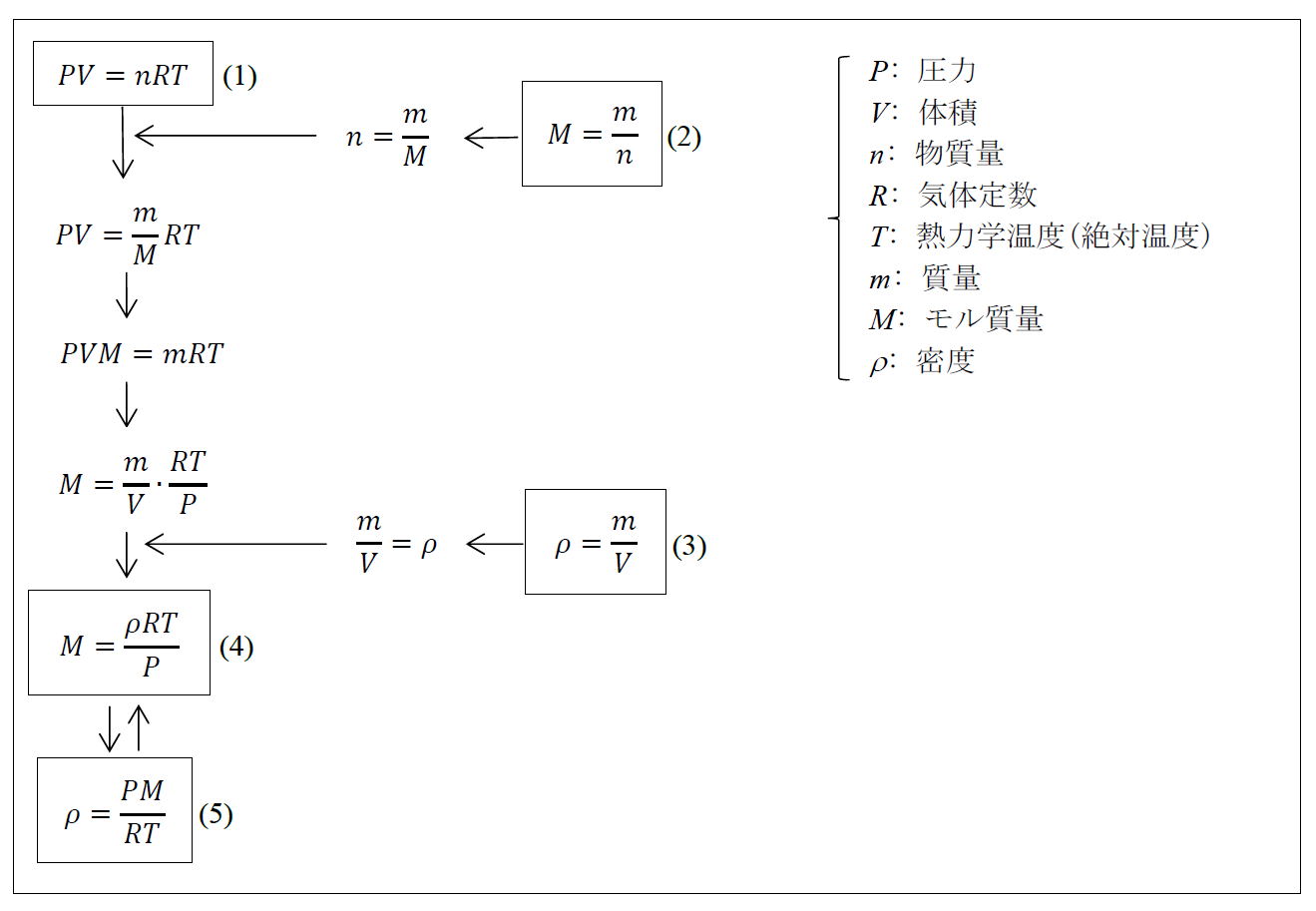
　(1)は理想気体の状態方程式、(2)はモル質量の定義、(3)は密度の定義である。(2)を変形した式より物質量を消去し、(3)を変形した式より質量および体積を消去すると、(4)および(5)が得られる。

【(4)の応用例】
　1.01×10⁵ Pa、118 ℃における酢酸蒸気の密度は3.2 g dm^-3であり、単量体(分子量60)と二量体の混合物であることが知られている。酢酸蒸気が理想気体として振舞うとして、このときの混合気体中の二量体の物質量分率を求める。

　原子量表(2022)の4桁の原子量の値より、H: 1.008、C: 12.01、O:16.00。よって、酢酸(C₂H₄O₂)のモル質量は、
(12.01×2＋1.008×4＋16.00×2) g mol^-1≒60.0 g mol^-1。
　平均モル質量を\(\bar{M}\)とすると、(4)より、

混合気体中での二量体の物質量分率を\(x\)とすると、

　よって、
60.0\(x\)＋60.0＝102.9

【(5)の応用例】
　空気が、同温・同圧での窒素対酸素の体積比が4:1の混合気体で、かつ理想気体として振舞うとして、1.01×10⁵ Pa、25 ℃での空気の密度を求める。

　まず、原子量表(2022)の4桁の原子量の値より、窒素および酸素のモル質量を求める。
N₂: (14.01×2) g mol^-1 ＝ 28.02 g mol^-1
O₂: (16.00×2) g mol^-1 ＝ 32.00 g mol^-1
よって、空気の平均モル質量\(\bar{M}\)は、

ゆえに、(5)より、

戻る